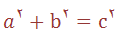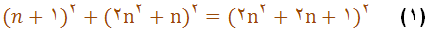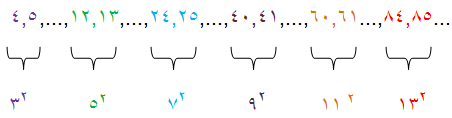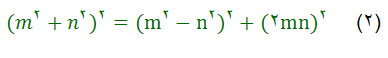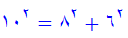|
گاه نوشته های یک دبیر ریاضی اینجا وبلاگ ریاضی صدای ما را از اردبیل می شنوید.
|
||
|
|
نوشته شده در تاريخ جمعه ۲۸ بهمن ۱۳۹۰
توسط پیله ور
چند تا سوال هوش ریاضی داشتم میشه برام حلش کنید!
1.امروز شنبه است و 3 دانش اموز برای مطالعه به کتابخانه رفتن.یکی از از دانش اموزان هر 3روز یکبار و دیگری هر 4 روز یکبار و سومی هر 6 روز به کتابخانه میرن؟تعیین کنید چند روز دیگر این سه دانش اموز در یک روز شنبه با هم در کتابخانه خواهند بود؟ --------------------------------------------------------------------------------------------------------- 2.سه رقمی را که در جمع زیر با X و y و Z نشان داده شده اند پیدا کنید؟ X X X X + y y y y Z Z Z Z -------------- y X X X Z ------------------------------------------------------------------------------------------ 3.فقط یک بار با استفاده از رقم های 0 تا 9 دو عدد پنج رقمی بنویسید که تفاضل ان ها حداقل باشد؟ ---------------------------------------------------------------------------------------------------- اگه جواب هاشو تو وبلاگتون برام بذارید ممنون میشم منتظرم! این مضمون سوالیه که در بخش نظرات توسط یکی از دانش آموزان پرسیده شده است .بد نیست شما هم به جواب مسئله ها فکر کنید. جواب در ادامه مطلب ادامه مطلب نوشته شده در تاريخ جمعه ۲۸ بهمن ۱۳۹۰
توسط پیله ور
همانطور كه خيلي ها تونسته بودند حل كنند جواب ۱۴۴ بود. حالا اينكه كساني كه تونسته اند اين سوال رو حل كنند واقعا بهره هوشي بالاتر از ۱۲۰ دارند جاي بحث دارند.در هر حال خوشحالم عده اي تونستند جواب رو پيدا کنند.
نوشته شده در تاريخ چهارشنبه ۲۶ بهمن ۱۳۹۰
توسط پیله ور
معما و روانشناسی به عمليات زير خوب دقت كنيد، مي گويند مي گويند تنها افراد با ضريب هوشي 120 يا بالاتر مي توانند پاسخ آن را بيايند! اگر 2 + 3 = 10 7 + 2 = 63 6 + 5 = 66 8 + 4 = 96 آنگاه 9 + 7 =???? جوابش رو هفته ديگه مي زارم.تا اون روز فكر كنيد. اين سوال رو يكي از دانش آموزان تو كلاس برام آورد. نوشته شده در تاريخ جمعه ۲۱ بهمن ۱۳۹۰
توسط پیله ور
جواب جالب دانش آموزان به سوال ریاضی برای دخترای دبیرستانیم
نوشته شده در تاريخ سه شنبه ۱۸ بهمن ۱۳۹۰
توسط پیله ور
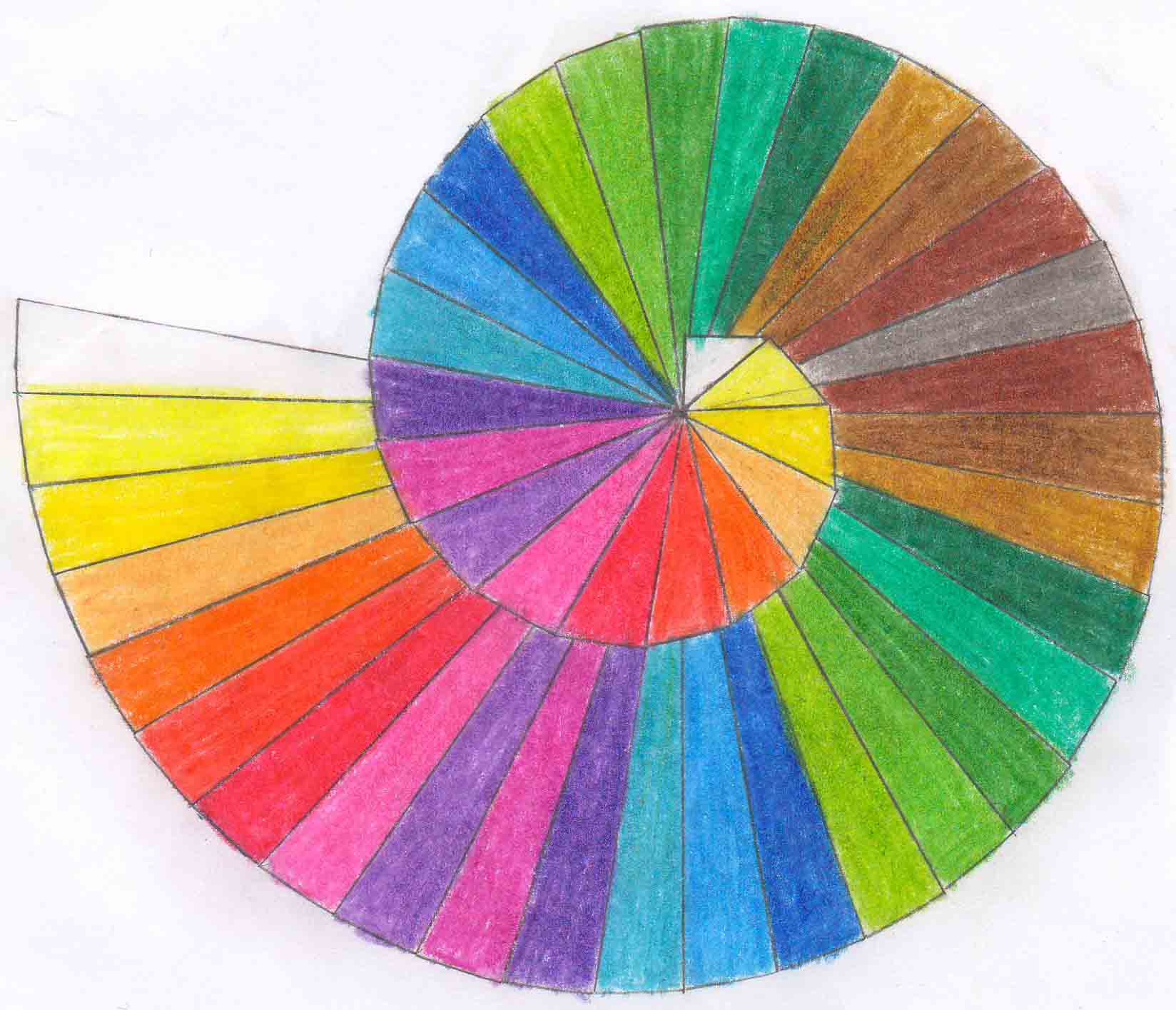
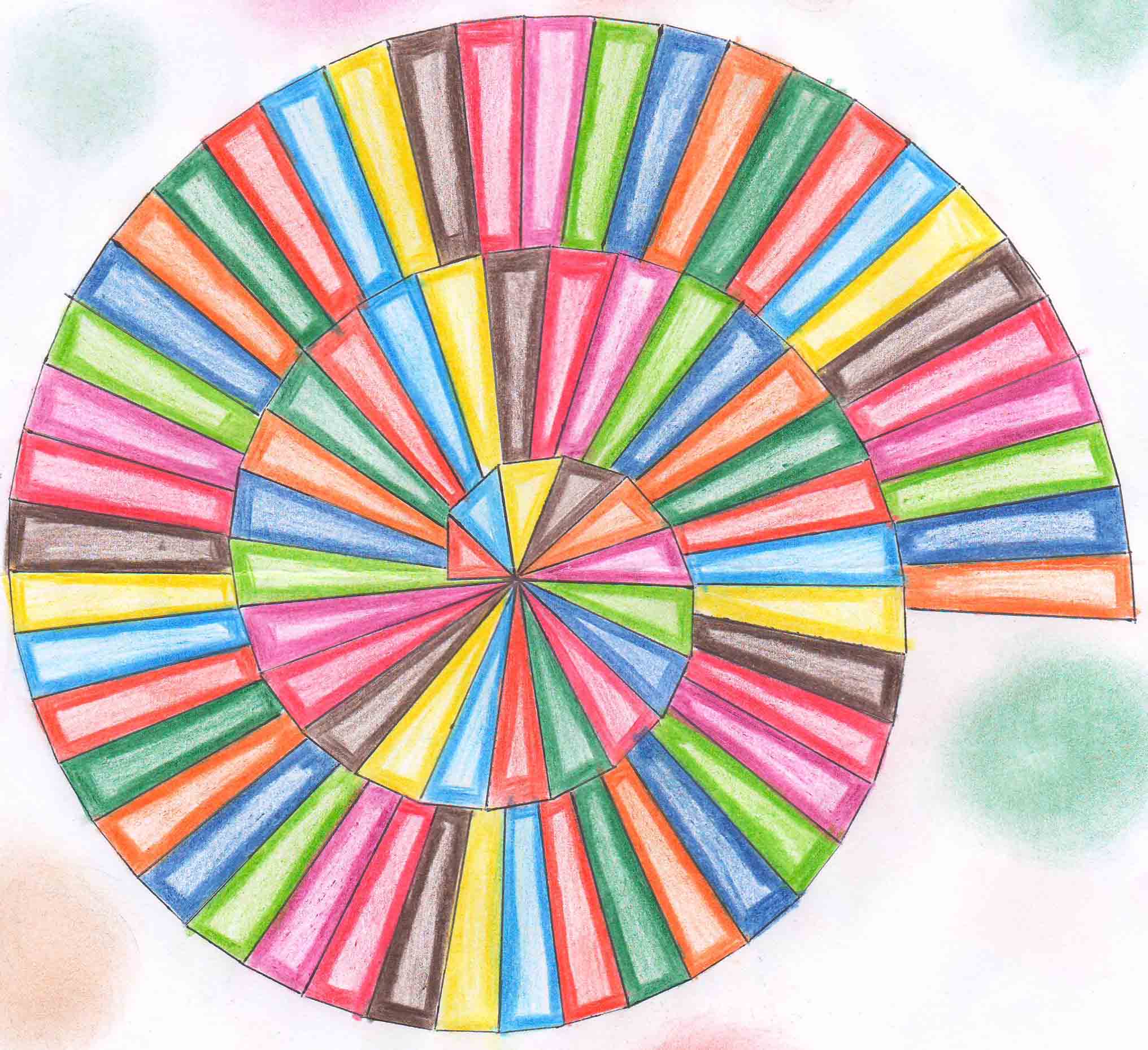
نمونه رسم دانش آموزان که بسیار زیبا رنگ کرده بودند.
فاطمه شیری
فاطمه باقری برای دیدن سایز بزرگتر روی اسامی کلیک کنید. نوشته شده در تاريخ سه شنبه ۱۸ بهمن ۱۳۹۰
توسط پیله ور

source:دنياي رياضي نوشته شده در تاريخ شنبه ۸ بهمن ۱۳۹۰
توسط پیله ور
مثلثهای فیثاغورثی
قبلا قول داده بودم مطلبی در مورد مثلثهای فیثاغورثی بزارم. حالا به بررسي مثلثهاي فيثاغورثي مي پردازيم ٬ يعني مثلثهايي كه ضلعهاي a٬b٬c آنها عددهاي صحيح باشند و در رابطه زير صدق كنند: همانطور كه مي دانيم چنين مثلثي قائم الزاويه است . روشن است كه اگر دو تا از اين عددها مقسوم عليه مشتركي داشته باشند٬عدد سوم هم بر اين مقسم عليه قابل قسمت خ.اهد بود .به همين مناسبت در بحث زير تنها از عددهاي صحيحي صحبت خواهيم كرد كه مقس.م عليه مشتركي (بجز واحد ) نداشته باشند. فيثاغورث قاعده اي را به دست اورده بود كه طبق آن بتوان عددهاي صحيحي براي مثلثهاي فيثاغورثي بدست آورد . با علامت گذاريهاي امروزي ٬ اين قاعده با تساوي زير بيان مي شود:
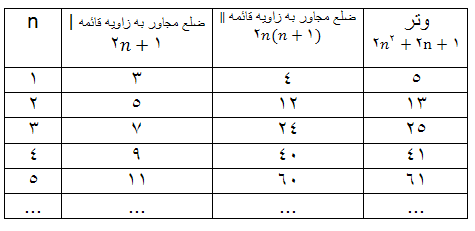
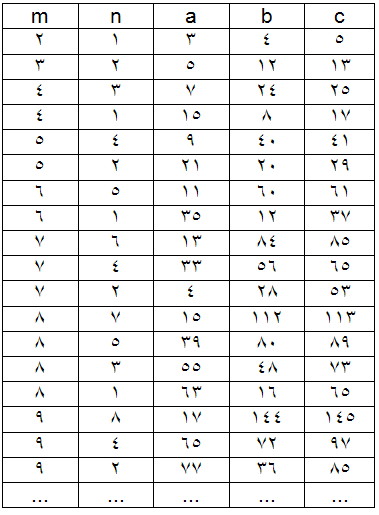
كه بجاي n مي توان هر عدد طبيعي دلخواه قرار داد. جدول زير بر اساس اين قاعده تنظيم شده است: از تساوي (1) و در جدول ديده مي شود: عددهايي كه ضلع مجاور به ضلع قائمه ∥ و وتر را معين مي كنند٬ دو عدد متوالي طبيعي هستند.به اين تر تيب مي توان گفت كه اگر در رشته عددهاي طبيعي به دو عدد متوالي بر خورد كنيم كه مجموع آنها مجذور كامل باشد ٬ اين دو عدد همراه با جذر مجموع آنها٬ سه ضلع مثلث فيثاغورثي را مشخص مي كنند: علاوه بر تساوي (1) ٬تساويهاي ديگري هم براي معين كردن عددها فيثاغورثي وجود دارد كه دير تر پيدا شده است. در اين رابطه مي توان بجاي mوnهر عدد دلخواه صحيح قرار داد. مثلا اگر m=3 وn=1بگيريم بدست مي آيد: يعني تر كيبي از عددهاي 6٬8,10 بدست مي ايد كه در جدول قبل وجود نداشت. به همين مناسبت رابطه (2) كلي تر از رابطه (1) به نظر مي رسد. ولي مطلب از اين جدي تر است.رابطه (2) شامل تمام انواع ممكنه عددهاي سه گانه فيثاغورثي است. اگر بخواهيم مثلثهاي متشابه فيثاغورثي تكرار نشود (مثلا دو مثلث 3٬4٬5 و 6٬8٬10 متاشابه اند.)بايد قاعده هاي زير را رعايت كنيم: 1) از دو عدد mوn بايد يكي فرد و ديگري زوج باشد٬ 2) بايد دو عدد mوn نسبت به يكديگر اول باشند٬ يعني مقسوم عليه مشتركي بجز واحد نداشته باشند٬ 3) جدولي را كه در آن اين قاعده ها رعايت شده است ٬ در زير مي آوريم: بر گرفته از : در پي فيثاغورث نوشته: شه پان النسكي نوشته شده در تاريخ جمعه ۷ بهمن ۱۳۹۰
توسط پیله ور
نوشته شده در تاريخ چهارشنبه ۵ بهمن ۱۳۹۰
توسط پیله ور
دیروز یکی از دانش اموزان در بخش نظرات این سوال رو ازم پرسیده.
«در یکی از سایتها در مورد رابطه فیثاغورس خوندم که از نظر فیثاغورس هرگاه مثلثی با نسبت های 3 و 4 و 5 ساخته بشه حتما قائم الزاویه است یعنی فرقی نمیکنه اندازه ضلع ها چقدر باشه مهم اینه که نسبت هاش به یک اندازه تغییر کنن مثلا مثلثی با اضلاع 6 و 8 و 10 قائم الزاویه است چون اگه ساده کنیم بازم نسبت هاش 3 و 4 و 5 میشه! حالا سوالم اینه در یک مثلث قائم الزاویه اندازه دو ضلع مجاور زاویه 90 درجه به ترتیب 5 و 12 سانتی متر است و اندازه ضلع سوم(وتر) 13 سانتی متر و رابطه فیثاغورس هم در این مثلث صدق میکنه! اضلاع این مثلث را چطور ساده کنیم که بازم نسبت ها 3 و 4 و 5 باشه؟خیلی فکر کردم ولی نتونستم حل کنم لطفا جوابش رو در اولین فرصت برام تو وبلاگتون قرار دهید چون خیلی برام مهمه! ممنون میشم منتظر جوابتون در وبلاگتون هستم.» عزیزم قضیه فیثاغورث میگه: «در هر مثلث قائم الزاویه مجذور وتر برابر است با مجموع مجذورهای دو ضلع دیگر.» حالا اعداد ۳ و۴و۵ یکی از اندازه هایی است که در قضیه فیثاغورث صدق می کنه پس مثلثی با اندازه های ۳و۴و۵ مثلثی قائم الزاویه است.پس هر اندازه ای با این نسبت نیز قائم الزاویه است.ولی عکس این مطلب درست نیست .یعنی نمی توانیم بگیم هر مثلثی نسبت ضلعهایش ۳و۴و۵ نباشد قائم الزاویه نیست.ممکنه نسبت اندازه ضلعهای مثلث ۳و۴و۵ نباشد ولی قائم الزاویه باشد. اندازه های دیگری نیز هستند که در قضیه فیثاورث صدق می کنند.همه مثلث های قائم الزاویه با اندازه های ۳و۴و۵ نیستند.ما بی نهایت مثلث قائم الزاویه با اندازه های مختلف می توانیم بکشیم.مثل همین موردی که شما نیز اشاره کردید. اندازه ۵و۱۲و۱۳ یا مثلثی با اندازه ۷و۲۴و۲۵ یا ۹و۴۰و۴۱ یا ۱۵و۸و۱۷ و ... امیدوارم تونسته باشم جواب قانع کننده ای برات گذاشته باشم . در اولین فرصت مطلبی در مورد اعداد فیثاغورثی یا مثلث های فبثاغورثی میزارم تا اطلاعاتت تکمیل بشه. و خودت بتونی هر سه عددی که مثلث قائم الزاویه تشکیل می دهند رو حدس بزنی. نوشته شده در تاريخ یکشنبه ۲ بهمن ۱۳۹۰
توسط پیله ور
|
|
| تمامی حقوق این وبلاگ محفوظ است | طراحی : پیچک | ||

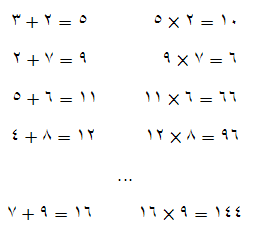
.jpg)