قبلا قول داده بودم مطلبی در مورد مثلثهای فیثاغورثی بزارم.

 حالا به بررسي مثلثهاي فيثاغورثي مي پردازيم ٬ يعني مثلثهايي كه ضلعهاي a٬b٬c   آنها عددهاي صحيح باشند و در رابطه زير صدق كنند:

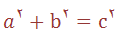
همانطور كه مي دانيم چنين مثلثي قائم الزاويه است . روشن است كه اگر دو تا از اين عددها مقسوم عليه مشتركي داشته باشند٬عدد سوم هم بر اين مقسم عليه قابل قسمت خ.اهد بود .به همين مناسبت در بحث زير تنها از عددهاي صحيحي صحبت خواهيم كرد كه مقس.م عليه مشتركي (بجز واحد ) نداشته باشند.

فيثاغورث قاعده اي را به دست اورده بود كه طبق آن بتوان عددهاي صحيحي براي مثلثهاي فيثاغورثي بدست آورد . با علامت گذاريهاي امروزي ٬ اين قاعده با تساوي زير بيان مي شود:

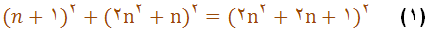
كه بجاي n مي توان هر عدد طبيعي دلخواه قرار داد.

  جدول زير بر اساس اين قاعده تنظيم شده است:

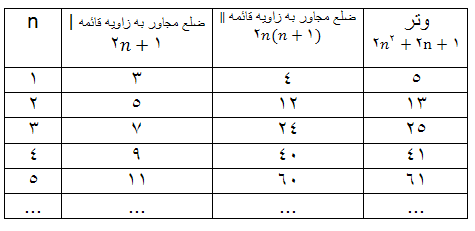
از تساوي (1) و در جدول ديده مي شود: عددهايي كه ضلع مجاور به ضلع قائمه ∥ و وتر را معين مي كنند٬ دو عدد متوالي طبيعي هستند.به اين تر تيب مي توان گفت كه اگر در رشته عددهاي طبيعي به دو عدد متوالي بر خورد كنيم كه مجموع آنها مجذور كامل باشد ٬ اين دو عدد همراه با جذر مجموع آنها٬ سه ضلع مثلث فيثاغورثي را مشخص مي كنند:

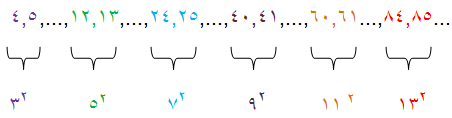
علاوه بر تساوي (1) ٬تساويهاي ديگري هم براي معين كردن عددها فيثاغورثي وجود دارد كه دير تر پيدا شده است.

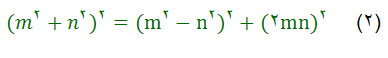
در اين رابطه مي توان بجاي mوnهر عدد دلخواه صحيح قرار داد. مثلا اگر m=3 وn=1بگيريم بدست مي آيد:     

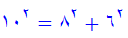
يعني تر كيبي از عددهاي 6٬8,10 بدست مي ايد كه در جدول قبل وجود نداشت. به همين مناسبت رابطه (2) كلي تر از رابطه (1) به نظر مي رسد.

ولي مطلب از اين جدي تر است.رابطه (2) شامل تمام انواع ممكنه عددهاي سه گانه فيثاغورثي است. اگر بخواهيم مثلثهاي متشابه فيثاغورثي تكرار نشود (مثلا دو مثلث 3٬4٬5 و 6٬8٬10 متاشابه اند.)بايد قاعده هاي زير را رعايت كنيم:

1)   از دو عدد mوn بايد يكي فرد و ديگري زوج باشد٬

2)   بايد دو عدد mوn نسبت به يكديگر اول باشند٬ يعني مقسوم عليه مشتركي بجز واحد نداشته باشند٬

3) 

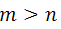
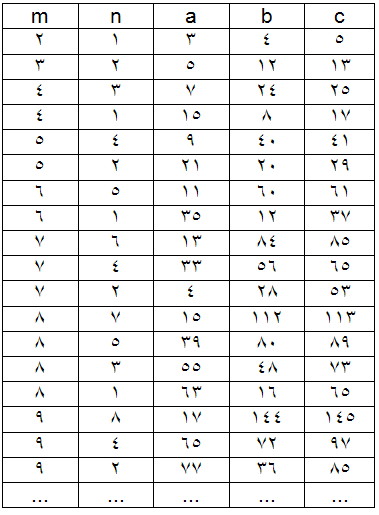
جدولي را كه در آن اين قاعده ها رعايت شده است ٬ در زير مي آوريم:

 بر گرفته از :

در پي فيثاغورث نوشته: شه پان النسكي